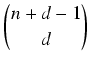
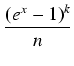
| S(n, n) = 1 dla n |
| S(n, k) = S(n - 1, k - 1) + kS(n - 1, k). |
B(n) = 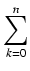 S(n, k).
S(n, k).
Liczby B(n) nazywamy liczbami Bella. Liczby Bella można obliczać rekurencyjnie:
B(n + 1) = 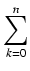
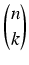 B(k)
B(k)
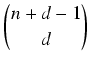
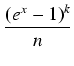
| S(n, n) = 1 dla n |
| S(n, k) = S(n - 1, k - 1) + kS(n - 1, k). |