


Next: Geometria analityczna na płaszczyźnie
Up: Rozwiązywanie trójkątów dowolnych
Previous: Rozwiązywanie trójkątów dowolnych
Niech dany będzie trójkąt o bokach a, b, c i niech p oznacza połowę obwodu tego trójkąta:
p = 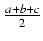 .
Udowodnimy wzór Herona na pole powierzchni trójkąta:
.
Udowodnimy wzór Herona na pole powierzchni trójkąta:
S =
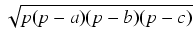
.
Niech 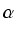 oznacza miarę kąta między bokami b i c i niech h będzie wysokością opuszczoną
na bok c. Wówczas:
oznacza miarę kąta między bokami b i c i niech h będzie wysokością opuszczoną
na bok c. Wówczas:
h =
b sin
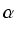
i wobec tego wzór na pole S trójkąta wyrazi się wzorem:
Wykorzystamy ten wzór. Najpierw występujący w nim
sin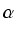 wyrazimy przez długości boków (korzystamy tu
z twierdzenia kosinusów):
wyrazimy przez długości boków (korzystamy tu
z twierdzenia kosinusów):
sin2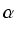 |
= |
1 - cos2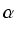 = 1 - ( = 1 - (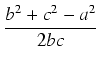 )2 = )2 = |
|
| |
= |
(1 + 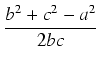 )(1 - )(1 - 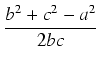 ) = ) = |
|
| |
= |
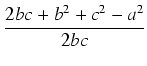 . . 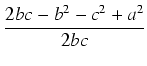 = = |
|
| |
= |
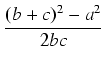 . . 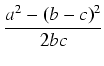 = = |
|
| |
= |
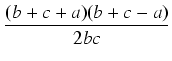 . . 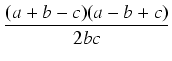 |
|
Ponieważ p oznacza połowę obwodu, więc
a + b + c = 2p a stąd:
| a + b - c |
= |
2p - 2c = 2(p - c) |
| a - b + c |
= |
2p - 2b = 2(p - b) |
| - a + b + c |
= |
2p - 2a = 2(p - a) |
i tym samym wzór na kwadrat sinusa przepisze się jako:
sin2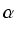 |
= |
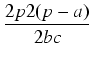 . . 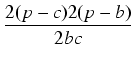 = = |
|
| |
= |
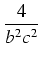 p(p - a)(p - b)(p - c) p(p - a)(p - b)(p - c) |
|
i ostatecznie:
skąd dostajemy wzór Herona.



Next: Geometria analityczna na płaszczyźnie
Up: Rozwiązywanie trójkątów dowolnych
Previous: Rozwiązywanie trójkątów dowolnych
Pawel Gladki
2006-01-30
![]() .
Udowodnimy wzór Herona na pole powierzchni trójkąta:
.
Udowodnimy wzór Herona na pole powierzchni trójkąta:
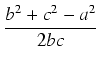 )2 =
)2 =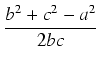 )(1 -
)(1 - 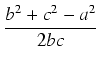 ) =
) =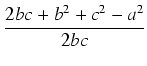 .
. 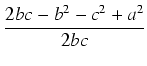 =
=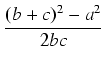 .
. 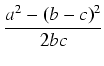 =
=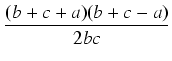 .
. 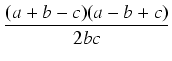
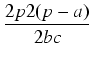 .
. 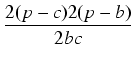 =
=