a) Reguła przybliżonego rozwiązywania równań zwana REGUŁĄ FALSI 
          posługuje się siecznymi.

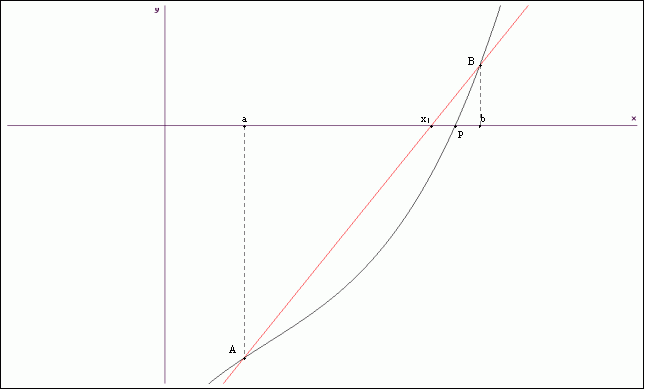
          Jeżeli, jak na rysunku, f(a)<0 i f(b)>0 ,  to równanie f(x)=0 
          ma w przedziale (a,b) pierwiastek p.

          Odcięta punktu przecięcia siecznej AB z osią x daje lepsze
          przybliżenie liczby p, niż jedna z liczb a i b.

          Oblicz tę odciętą z równania siecznej.

          Możemy teraz obliczyć i jeśli  to mamy sytuację taką
          jak na początku, ale dla przedziału .

          W przeciwnym przypadku rozpatrujemy przedział .

            Kliknij na obrazek i zaobserwuj co się dzieje, gdy zastosujemy tę regułę zaledwie 3 razy!

       Widać, że x₃ jest już bardzo dobrym przybliżeniem liczby p.

       Kolejne wyniki będą coraz dokładniejszym przybliżeniem pierwiastka p.      

     b) Metoda przybliżonego rozwiązywania równań zwana METODĄ
         NEWTONA posługuje się styczną. 
         Dotyczy ona sytuacji takiej jak na rysunku.

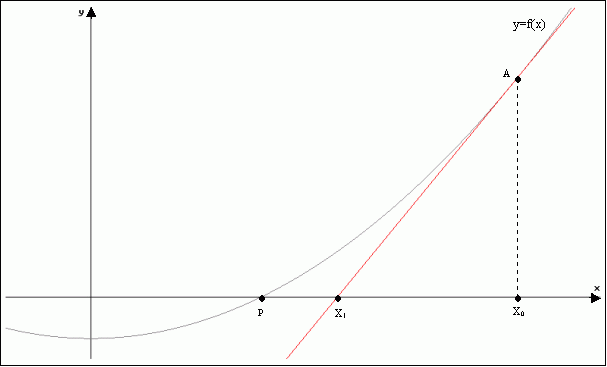
         Równanie f(x)=0 ma pierwiastek p.

         Odcięta   punktu przecięcia stycznej w punkcie   wykresu
         z osią x, lepiej przybliża pierwiastek p niż liczba .        

        Oblicz odciętą z równania stycznej.

           Kliknij na obrazek i zaobserwuj co się dzieje, gdy zastosujemy tę regułę 3 razy!

        Widać, że x₃ jest już bardzo dobrym przybliżeniem liczby p. 

        Powtarzając tę procedurę wielokrotnie otrzymujemy ciąg coraz
        lepszych przybliżeń pierwiastka p: