Na zamieszczonych rysunkach funkcja przedstawiona jest
kolorem niebieskim, zaś jej pochodna
kolorem czerwonym.
Funkcje stałe (niemonotoniczne) przedstawione na rysunkach mają pochodne równe zero.
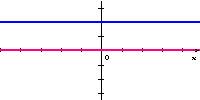
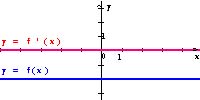
W przypadku innych funkcji stałych będzie podobnie.
Pochodna funkcji stałej jest funkcją stałą równą zero.
Czy potrafisz to uogólnić ? Jakim wzorem wyraża się pochodna funkcji f(x) = a, a € R ?
Wniosek 1.
Pochodną funkcji stałej f(x) = a, a € R jest funkcja stała f ' (x) = 0.
Popatrz na wykresy funkcji liniowych i wykresy ich pochodnych.
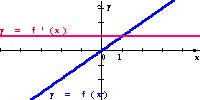
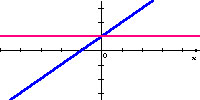
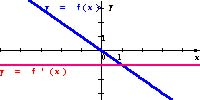
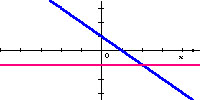
Zauważ, że
Pochodną funkcji liniowej jest funkcja stała.
Czy potrafisz odczytać z wykresów wzory, jakimi opisane są narysowane funkcje liniowe ?
Spróbujmy to uogólnić.
Pochodną funkcji liniowej określonej wzorem y = ax + b, a € R \ {0}, jest funkcja stała określona wzorem
Wniosek 2.
Pochodną funkcji liniowej f(x) = ax + b,
a € R \ {0} jest funkcja stała f ' (x) = a, a € R \ {0}.
Popatrzmy teraz na funkcję kwadratową.
Wykresem funkcji kwadratowej jest parabola.
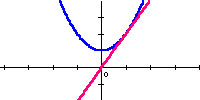
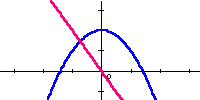
Wykresem funkcji pochodnej jest prosta, czyli
pochodna funkcji kwadratowej jest funkcją liniową.
Spróbuj odkryć zależność między wzorami funkcji kwadratowej i jej pochodnej.
Popatrz na wykresy. Odczytaj wzory określające funkcję i jej pochodną.
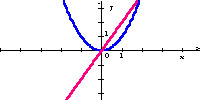y = x2
y' = x
y = 2x2
y' = 2x
y = -x2
y' = 0,5x
y = 0,5x2
y' = - x
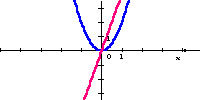y = x2
y' = x
y = 2x2
y' = 2x
y = -x2
y' = 4x
y = 0,5x2
y' = - x
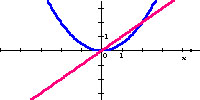y = x2
y' = x
y = 2x2
y' = 2x
y = 0,5x2
y' = 4x
y = - x2
y' = -x
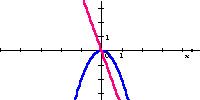y = x2
y' = x
y = -x2
y' = -2x
y = 0,5x2
y' = -4x
y = -2x2
y' = -x
Czy potrafisz już sformułować wniosek ? Jakim wzorem określona jest pochodna funkcji y = ax2 (a € R \ {0}) ?
Wniosek 3.
Popatrzmy jeszcze na wielomiany stopnia trzeciego i ich pochodne.
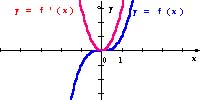
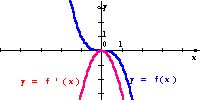
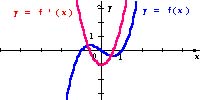
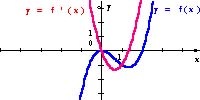
Możesz zaobserwować, że
Pochodna wielomianu stopnia trzeciego jest wielomianem stopnia drugiego. #
Dla wielomianów istnieją ich pochodne.Wielomian jest funkcją różniczkowalną
Można udowodnić twierdzenie 8 o stopniu pochodnej wielomianu.