
Dziś jesteśmy w stanie obliczyć wartość p aż do milionów miejsc po przecinku, ale ciągle szukamy odpowiedzi na pytanie - jakiego rodzaju to liczba ?
Znaczna część historii związanej z liczbą p składa sie ze stwierdzeń, iż wartość tej liczby jest równa lub bliska jakiejś innej liczbie.
 Matematyczna historia liczby p
zaczyna się od Archimedesa. Pokazał on, że:
Matematyczna historia liczby p
zaczyna się od Archimedesa. Pokazał on, że:
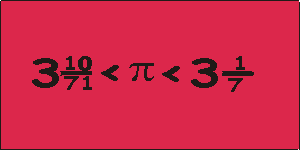
W tym celu obliczał pola zawarte w wielokącie foremnym o 96 bokach, a w swych pomysłowych obliczeniach korzystał z przybliżeń pierwiastków kwadratowych.
 Chiński astronom Tsu Chung-chih (urodzony w 430r. n. e.) podał już "przybliżoną wartość" liczby p tzn.: 22/7 oraz lepsze ograniczenie: 3,1415926, niż wiedzieli to jeszcze p. n. e. - Babilończycy (3 i 1/8) czy Egipcjanie (3,1605).
Chiński astronom Tsu Chung-chih (urodzony w 430r. n. e.) podał już "przybliżoną wartość" liczby p tzn.: 22/7 oraz lepsze ograniczenie: 3,1415926, niż wiedzieli to jeszcze p. n. e. - Babilończycy (3 i 1/8) czy Egipcjanie (3,1605).
 W 1585r. niejaki Adrian Metius odkrył, że:
W 1585r. niejaki Adrian Metius odkrył, że:
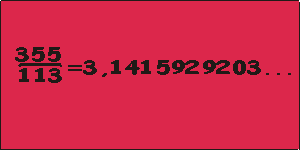
ale okazało się, że nawet ta liczba nie określa dokładnie wartości p.

 W 1593 roku Vieta podał wzór na p:
W 1593 roku Vieta podał wzór na p:
Doszedł do niego, stosując pomysł Archimedesa do wielokątów o bokach 4, 8, 16, ..., 2n, wpisanych w okrąg o promieniu 1.
 Dużą część swego życia na obliczeniach liczby p spędził niemiecki matematyk Ludolf van Ceulen; w Niemczech do dziś liczbę
p nazywa się niekiedy liczbą Ludolfa (w języku polskim istnieje nazwa ludolfina, choć rzadko używana).
Dużą część swego życia na obliczeniach liczby p spędził niemiecki matematyk Ludolf van Ceulen; w Niemczech do dziś liczbę
p nazywa się niekiedy liczbą Ludolfa (w języku polskim istnieje nazwa ludolfina, choć rzadko używana).
Van Ceulen nakazał, by wyryto ją na jego nagrobku - dziś, niestety, zaginionym. W 1596 roku obliczył on wartość
p z dokładnością do 20 miejsc po przecinku, a przed śmiercią zdążył jeszcze poprawić dokładność swoich obliczeń do 35 miejsca po przecinku:
Niedługo po jego śmierci nowe odkrycia spowodowały obfitość wzorów na wartość liczby p, a niektóre z nich pozwalają obliczyć ją bardzo szybko.
 Czy jest możliwe, żeby p była dokładnie równa pewnemu ułamkowi? Odpowiedź brzmi: "nie", jak pokazał wielki matematyk niemiecki Lambert w 1761roku. Lambert udowodnił również, że p nie jest nawet pierwiastkiem kwadratowym żadnego ułamka.
Czy jest możliwe, żeby p była dokładnie równa pewnemu ułamkowi? Odpowiedź brzmi: "nie", jak pokazał wielki matematyk niemiecki Lambert w 1761roku. Lambert udowodnił również, że p nie jest nawet pierwiastkiem kwadratowym żadnego ułamka.
 Wielu matematyków musiało podejrzewać, iż p nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych, co oznaczałoby, że jest liczbą przestępną. Dowód tego faktu, podany przez Lindemanna w 1882 roku, był jednym z kamieni milowych w rozwoju matematyki.
Wielu matematyków musiało podejrzewać, iż p nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych, co oznaczałoby, że jest liczbą przestępną. Dowód tego faktu, podany przez Lindemanna w 1882 roku, był jednym z kamieni milowych w rozwoju matematyki.
 POWRÓT
POWRÓT


 Matematyczna historia liczby p
zaczyna się od Archimedesa. Pokazał on, że:
Matematyczna historia liczby p
zaczyna się od Archimedesa. Pokazał on, że:
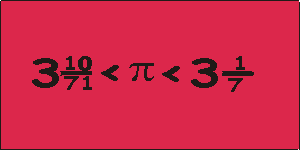
 Chiński astronom Tsu Chung-chih (urodzony w 430r. n. e.) podał już "przybliżoną wartość" liczby p tzn.: 22/7 oraz lepsze ograniczenie: 3,1415926, niż wiedzieli to jeszcze p. n. e. - Babilończycy (3 i 1/8) czy Egipcjanie (3,1605).
Chiński astronom Tsu Chung-chih (urodzony w 430r. n. e.) podał już "przybliżoną wartość" liczby p tzn.: 22/7 oraz lepsze ograniczenie: 3,1415926, niż wiedzieli to jeszcze p. n. e. - Babilończycy (3 i 1/8) czy Egipcjanie (3,1605).  W 1585r. niejaki Adrian Metius odkrył, że:
W 1585r. niejaki Adrian Metius odkrył, że:
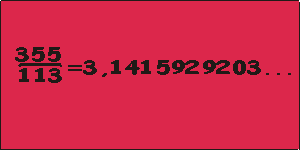

 W 1593 roku Vieta podał wzór na p:
W 1593 roku Vieta podał wzór na p:
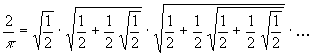
 Dużą część swego życia na obliczeniach liczby p spędził niemiecki matematyk Ludolf van Ceulen; w Niemczech do dziś liczbę
p nazywa się niekiedy liczbą Ludolfa (w języku polskim istnieje nazwa ludolfina, choć rzadko używana).
Dużą część swego życia na obliczeniach liczby p spędził niemiecki matematyk Ludolf van Ceulen; w Niemczech do dziś liczbę
p nazywa się niekiedy liczbą Ludolfa (w języku polskim istnieje nazwa ludolfina, choć rzadko używana).


 Czy jest możliwe, żeby p była dokładnie równa pewnemu ułamkowi? Odpowiedź brzmi: "nie", jak pokazał wielki matematyk niemiecki Lambert w 1761roku. Lambert udowodnił również, że p nie jest nawet pierwiastkiem kwadratowym żadnego ułamka.
Czy jest możliwe, żeby p była dokładnie równa pewnemu ułamkowi? Odpowiedź brzmi: "nie", jak pokazał wielki matematyk niemiecki Lambert w 1761roku. Lambert udowodnił również, że p nie jest nawet pierwiastkiem kwadratowym żadnego ułamka.  Wielu matematyków musiało podejrzewać, iż p nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych, co oznaczałoby, że jest liczbą przestępną. Dowód tego faktu, podany przez Lindemanna w 1882 roku, był jednym z kamieni milowych w rozwoju matematyki.
Wielu matematyków musiało podejrzewać, iż p nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych, co oznaczałoby, że jest liczbą przestępną. Dowód tego faktu, podany przez Lindemanna w 1882 roku, był jednym z kamieni milowych w rozwoju matematyki.
