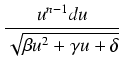Next: Całka oznaczona
Up: Rachunek całkowy
Previous: Całki funkcji zawierających pierwiastek
Metoda współczynników nieoznaczonych stosuje się do obliczania całek postaci:

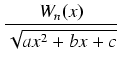 dx
dx,
gdzie Wn(x) jest wielomianem stopnie n, jest to więc jeszcze jedna metoda pozwalająca obliczać całki z funkcji zawierających pierwiastek z trójmianu
kwadratowego. Gdybyśmy chcieli zamieścić tę metodę w poprzednim rozdziale, jego tytuł za bardzo by się wydłużył
i strona z FAQ źle by się wyświetlała, dlatego zdecydowaliśmy się opisać ją w osobnym artykule :)
Całka powyższa równa się wyrażeniu:
gdzie
Wn-1(x) jest wielomianem stopnia n - 1, a A pewną stałą. Współczynniki wielomianu
Wn-1(x)
oraz stałą A obliczamy przyrównując
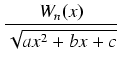
,
czyli pochodną funkcji będącej obliczaną całką do pochodnej powyższego wyrażenia.
Przykład: Obliczyć całkę:

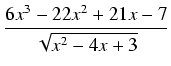 dx
dx.
Przewidujemy, że całka nasza będzie równa wyrażeniu następującej postaci:
Aby obliczyć współczynniki
a, b, c, A różniczkujemy powyższe wyrażenie i przyrównujemy do funkcji podcałkowej:
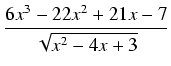
= (2
ax +
b)
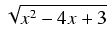
+ (
ax2 +
bx +
c)
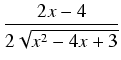
+
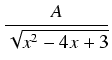
.
Mnożymy obie strony tożsamości przez
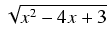 :
:
6x3 -22x2 +21x - 7 = (2ax + b)(x2 -4x + 3) + (ax2 + bx + c)(x - 2) + A
i obliczamy współczynniki porównując wyrażenia przy kolejnych potęgach zmiennej x.
Przykład: Obliczyć całkę:

(3
x - 2)
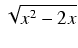 dx
dx.
W tym przypadku funkcję podcałkową mnożymy i dzielimy przez
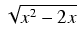 otrzymując:
otrzymując:

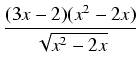 dx
dx
i dalej postępujemy podobnie, jak w poprzednim przykładzie.
Przykład: Obliczyć całkę:

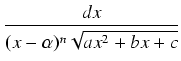
.
W tym przypadku stosujemy podstawienie
u = 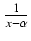 i otrzymujemy całkę postaci:
i dalej postępujemy zgodnie z opisaną metodą.
i otrzymujemy całkę postaci:
i dalej postępujemy zgodnie z opisaną metodą.
Ćwiczenia:
-

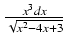 Odpowiedź:
Odpowiedź:
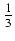 (x2 +5x + 24)
(x2 +5x + 24)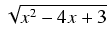 +11ln| x - 2 +
+11ln| x - 2 + 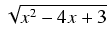 | + C
| + C
-

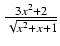 dx Odpowiedź:
dx Odpowiedź:
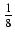 (8x2 -10x - 1)
(8x2 -10x - 1)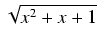 +
+ 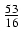 ln| x +
ln| x + 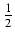 +
+ 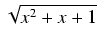 | + C
| + C
-
 x2
x2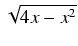 dx Odpowiedź:
dx Odpowiedź:
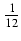 (3x3 -2x2 -10x - 60)
(3x3 -2x2 -10x - 60)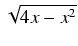 +10arcsin
+10arcsin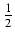 (x - 2) + C
(x - 2) + C
-
 x
x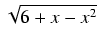 dx Odpowiedź:
dx Odpowiedź:
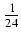 (8x2 -2x - 51)
(8x2 -2x - 51)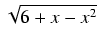 -
- 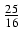 arcsin
arcsin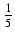 (1 - 2x) + C
(1 - 2x) + C
-

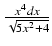 Odpowiedź:
Odpowiedź:
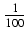 (5x3 -6x)
(5x3 -6x)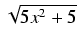 +
+ 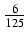
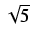 ln| x
ln| x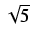 +
+ 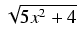 | + C
| + C



Next: Całka oznaczona
Up: Rachunek całkowy
Previous: Całki funkcji zawierających pierwiastek
Pawel Gladki
2006-01-30
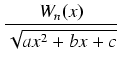 dx,
dx,
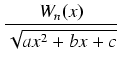 dx,
dx,
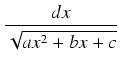 ,
,
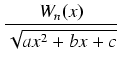 ,
,
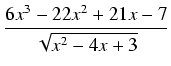 dx.
dx.
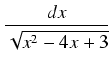 .
.
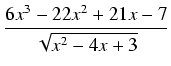 = (2ax + b)
= (2ax + b)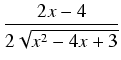 +
+ 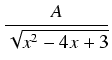 .
.
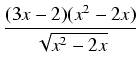 dx
dx
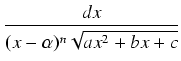 .
.