


Next: Całki z funkcji wymiernych
Up: Rachunek całkowy
Previous: Podstawowe wzory rachunku całkowego
Twierdzenie: Całka sumy równa się sumie całek, tzn.

(
f (
x) +
g(
x))
dx =
 f
f (
x)
dx +
 g
g(
x)
dx.
Stały czynnik wolno wynieść przed znak całki, tzn.
 kf
kf (
x)
dx =
k f
f (
x)
dx,
k 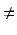
0.
Twierdzenie (o całkowaniu przez podstawienie): Jeżeli dla
a 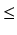 x
x 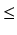 b funkcja g(x) = u jest
ciągła i ma ciągłą pochodną oraz
A
b funkcja g(x) = u jest
ciągła i ma ciągłą pochodną oraz
A 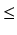 g(x)
g(x) 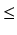 B, zaś funkcja f (u) jest ciągła w przedziale [A, B], to:
B, zaś funkcja f (u) jest ciągła w przedziale [A, B], to:
 f
f (
g(
x))
g'(
x)
dx =
 f
f (
u)
du,
przy czym po scałkowaniu prawej strony należy w otrzymanym wyniku podstawić u = g(x).
Twierdzenie (o całkowaniu przez części): Jeżeli u, v są funkcjami zmiennej x mającymi ciągła pochodną, to:
 u
u(
x)
v'(
x)
dx =
u(
x)
v(
x) -
 u'
u'(
x)
v(
x)
dx.
Przykład: Obliczyć całkę:

25
x7 +49
ex +
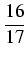 sinxdx
sinxdx.
Zgodnie z twierdzeniem o sumie całek i o całce pomnożonej przez skalar mamy:
 25x7+49ex+ 25x7+49ex+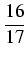 sinxdx=25 sinxdx=25 x7dx+49 x7dx+49 exdx+ exdx+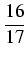  sinxdx= sinxdx= |
| |
= |
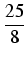 x8 +49ex - x8 +49ex - 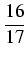 cosx + C cosx + C |
|
Przykład: Obliczyć całkę:
 tgxdx
tgxdx.
Skorzystamy z tożsamości
tgx = 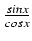 . Zatem obliczamy
. Zatem obliczamy

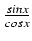 stosując
podstawienie
stosując
podstawienie
u = cosx.
Stąd różniczkując otrzymujemy
du = - sinxdx,
a zatem:

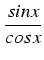 dx
dx = -

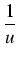 du
du = - ln|
u| +
C = - ln|
cosx| +
C.
Przykład: Obliczyć całkę:
 xsinxdx
xsinxdx.
Całkujemy przez części przyjmując
u(
x) =
x,
v'(
x) =
sinx skąd
u'(
x) = 1,
v(
x) =
 sinxdx
sinxdx = -
cosx.
Otrzymujemy:
 xsinxdx
xsinxdx = -
xcosx -

(-
cosx)
dx = -
xcosx +
 cosxdx
cosxdx = -
xcosx +
sinx +
C.
Ćwiczenia z zastosowaniem twierdzenia o całkowaniu przez podstawienie:
-

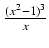 dx Odpowiedź:
dx Odpowiedź:
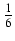 x6 -
x6 - 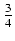 x4 +
x4 + 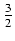 x2 - ln| x| + C
x2 - ln| x| + C
-

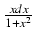 Odpowiedź:
Odpowiedź:
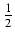 ln(1 + x2) + C
ln(1 + x2) + C
-

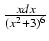 Odpowiedź:
Odpowiedź:
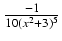 + C
+ C
-

![$ {\frac{{x dx}}{{\sqrt[3]{2x^2 - 1}}}}$](img337.gif) Odpowiedź:
Odpowiedź:
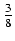 (2x2 -1)2/3 + C o ile
x
(2x2 -1)2/3 + C o ile
x 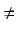
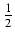
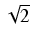 ,
x
,
x 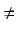 -
- 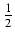
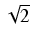
-
 xe-x2dx Odpowiedź:
-
xe-x2dx Odpowiedź:
- 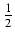 e-x2 + C
e-x2 + C
-
 xsin(2x2 + 1)dx Odpowiedź:
-
xsin(2x2 + 1)dx Odpowiedź:
- 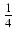 cos(2x2 + 1) + C
cos(2x2 + 1) + C
-

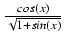 dx Odpowiedź:
2
dx Odpowiedź:
2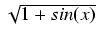 + C
+ C
-

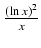 dx Odpowiedź:
dx Odpowiedź:
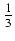 ln3x + C o ile x > 0
ln3x + C o ile x > 0
-
 x ln(1 + x2)dx Odpowiedź:
x ln(1 + x2)dx Odpowiedź:
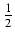 (1 + x2)ln(1 + x2) -
(1 + x2)ln(1 + x2) - 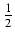 x2 + C
x2 + C
-

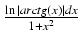 Odpowiedź:
arctg(x)(ln| arctg(x)| - 1) + C
Odpowiedź:
arctg(x)(ln| arctg(x)| - 1) + C
Dodatkowe ćwiczenia
Ćwiczenia z zastosowaniem twierdzenia o całkowaniu przez części:
-
 xe3xdx Odpowiedź:
xe3xdx Odpowiedź:
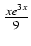 -
- 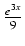 + C
+ C
-
 xsin(5x)dx Odpowiedź:
-
xsin(5x)dx Odpowiedź:
- 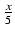 cos(5x) +
cos(5x) + 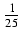 sin(5x) + C
sin(5x) + C
-
x2ln(x)dx Odpowiedź:
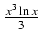 -
- 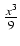 + C
+ C
-
x2e-5xdx Odpowiedź:
-
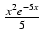 -
- 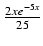 -
- 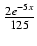 + C
+ C
-
x2cos(3x)dx Odpowiedź:
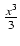 sin(3x) +
sin(3x) + 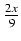 cos(3x) -
cos(3x) - 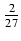 sin(3x) + C
sin(3x) + C
-
(x2 +2x + 1)e7xdx Odpowiedź:
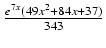 + C
+ C
-
 arctg(x)dx Odpowiedź:
xarctg(x) -
arctg(x)dx Odpowiedź:
xarctg(x) - 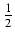 ln| 1 + x2| + C
ln| 1 + x2| + C
-
 sin5(x)dx Odpowiedź:
-
sin5(x)dx Odpowiedź:
- 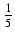 cos(x)sin4(x) -
cos(x)sin4(x) - 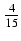 sin2(x)cos(x) -
sin2(x)cos(x) - 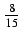 cos(x) + C
cos(x) + C
-
 x2arcctg(x)dx Odpowiedź:
x2arcctg(x)dx Odpowiedź:
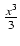 arcctg(x) +
arcctg(x) + 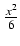 -
- 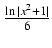 + C
+ C
-
 e9xcos(2x)dx Odpowiedź:
e9x(
e9xcos(2x)dx Odpowiedź:
e9x(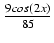 +
+ 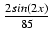 ) + C
) + C
Dodatkowe ćwiczenia



Next: Całki z funkcji wymiernych
Up: Rachunek całkowy
Previous: Podstawowe wzory rachunku całkowego
Pawel Gladki
2006-01-30
![]() x
x ![]() b funkcja g(x) = u jest
ciągła i ma ciągłą pochodną oraz
A
b funkcja g(x) = u jest
ciągła i ma ciągłą pochodną oraz
A ![]() g(x)
g(x) ![]() B, zaś funkcja f (u) jest ciągła w przedziale [A, B], to:
B, zaś funkcja f (u) jest ciągła w przedziale [A, B], to: