


Next: Rachunek całkowy
Up: Ciągi liczbowe
Previous: Ciągi liczbowe
Indukcja matematyczna
Indukcja matematyczna, zwana też indukcją zupełną, jest to metoda dowodzenia twierdzeń o liczbach
naturalnych.
Niech T(n) oznacza formę zdaniową zmiennej n określoną w dziedzinie
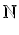 . Jeśli w miejsce n
podstawimy dowolną liczbę naturalną, to T(n) stanie się zdaniem prawdziwym albo fałszywym, zależnie
od wartości n. Jeżeli, na przykład, T(n) oznacza wypowiedź "n jest podzielne przez 3", to T(6)
jest zdaniem prawdziwym, natomiast T(7) jest zdaniem fałszywym. Jeżeli T(n) oznacza nierówność n < n2,
to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej większej od 1, natomiast zdanie T(1) jest
fałszywe.
. Jeśli w miejsce n
podstawimy dowolną liczbę naturalną, to T(n) stanie się zdaniem prawdziwym albo fałszywym, zależnie
od wartości n. Jeżeli, na przykład, T(n) oznacza wypowiedź "n jest podzielne przez 3", to T(6)
jest zdaniem prawdziwym, natomiast T(7) jest zdaniem fałszywym. Jeżeli T(n) oznacza nierówność n < n2,
to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej większej od 1, natomiast zdanie T(1) jest
fałszywe.
Metoda indukcji matematycznej opiera się na następującej zasadzie:
Zasada indukcji matematycznej. Jeżeli
- istnieje taka liczba naturalna n0, że T(n0) jest zdaniem prawdziwym,
- dla każdej liczby naturalnej
n
 n0 prawdziwa jest implikacja
T(n)
n0 prawdziwa jest implikacja
T(n) 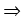 T(n + 1),
T(n + 1),
to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej
n  n0.
n0.
Przykład: Udowodnić, że dla każdej liczby naturalnej n  3 spełniona jest nierówność
3 spełniona jest nierówność
2n > 2n.
Nierówność jest tu formą zdaniową T(n), n0 = 3.
1. Dla n = 3 nierówność jest prawdziwa, ponieważ
23 = 8 > 2 . 3 = 6. T(3) jest więc zdaniem
prawdziwym.
2. Załóżmy, że nierówność jest prawdziwa dla liczby naturalnej n  3. Mnożąc tę nierówność obustronnie
przez 2 dostajemy
2 . 2n > 2 . 2n, czyli
2n+1 > 2n + 2n. Ponieważ dla każdego n
3. Mnożąc tę nierówność obustronnie
przez 2 dostajemy
2 . 2n > 2 . 2n, czyli
2n+1 > 2n + 2n. Ponieważ dla każdego n  3
mamy 2n > 2, więc
2n + 2n > 2n + 2 = 2(n + 1). Stąd ostatecznie
3
mamy 2n > 2, więc
2n + 2n > 2n + 2 = 2(n + 1). Stąd ostatecznie
2n+1 > 2(n + 1).
Nierówność ta oznacza prawdziwość zdania T(n + 1). Wykazaliśmy zatem, że dla każdej liczby naturalnej
n  3 prawdziwa jest implikacja
T(n)
3 prawdziwa jest implikacja
T(n) 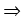 T(n + 1), gdyż z prawdziwości jej poprzednika wynika
prawdziwość następnika.
T(n + 1), gdyż z prawdziwości jej poprzednika wynika
prawdziwość następnika.
Ponieważ założenia zasady indukcji matematycznej są dla nierówności spełnione, więc ta nierówność jest
prawdziwa dla każdego n  3.
3.
Dowód przeprowadzony metodą indukcji matematycznej nazywamy dowodem indukcyjnym; składa się on
z dwóch etapów:
1. sprawdzenia, że T(n0) jest prawdziwe,
2. dowodu, że dla każdego
n  n0 jeżeli T(n) jest prawdziwe, to T(n + 1) jest prawdziwe.
n0 jeżeli T(n) jest prawdziwe, to T(n + 1) jest prawdziwe.
Ten drugi etap nazywamy krokiem indukcyjnym; zakładamy w nim, że dla liczby naturalnej
n  n0
zdanie T(n) jest prawdziwe (tzw. hipoteza indukcyjna) i na tej podstawie dowodzimy prawdziwości
zdania T(n + 1).
n0
zdanie T(n) jest prawdziwe (tzw. hipoteza indukcyjna) i na tej podstawie dowodzimy prawdziwości
zdania T(n + 1).
Oto jeszcze jeden przykład:
Przykład: Udowodnić, że dla każdego naturalnego n
1
2 +2
2 +...+
n2 =
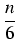
(
n + 1)(2
n + 1).
Dowód indukcyjny, n0 = 1.
1. Sprawdzamy, że równość jest prawdziwa dla n = 1:
1
2 =
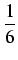
(1 + 1)(2
. 1 + 1) = 1.
2. Załóżmy, że równość jest prawdziwa dla liczby naturalnej n. Do obu stron tej równości dodajemy
(n + 1)2, więc
1
2 +2
2 +...+
n2 + (
n + 1)
2 =
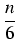
(
n + 1)(2
n + 1) + (
n + 1)
2
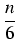 (n+1)(2n+1)+(n+1)2= (n+1)(2n+1)+(n+1)2=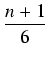 [n(2n+1)+6(n+1)]= [n(2n+1)+6(n+1)]= |
| |
= |
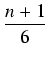 (2n2 +7n + 6) = (2n2 +7n + 6) = 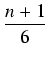 (n + 2)(2n + 3). (n + 2)(2n + 3). |
|
Stąd
1
2 +2
2 +...+
n2 + (
n + 1)
2 =
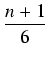
[(
n + 1) + 1]
. [2(
n + 1) + 1].
 T(n + 1),
gdzie T(n) oznacza dowodzoną równość. Na mocy zasady indukcji matematycznej równość jest więc prawdziwa
dla każdej liczby naturalnej n.
T(n + 1),
gdzie T(n) oznacza dowodzoną równość. Na mocy zasady indukcji matematycznej równość jest więc prawdziwa
dla każdej liczby naturalnej n.
Za pomocą zasady indukcji matematycznej łatwo i szybko dowodzi się cały szereg charakterystycznych
twierdzeń. Podajemy niektóre z nich.
Sumy potęg kolejnych liczb naturalnych.
-
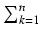 k =
k = 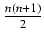 = s1
= s1
-
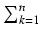 k2 =
k2 = 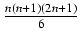 = s2 (patrz powyższy przykład)
= s2 (patrz powyższy przykład)
-
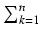 k3 = s12
k3 = s12
-
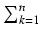 k4 =
k4 = 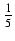 s2(3n2 + 3n - 1)
s2(3n2 + 3n - 1)
-
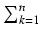 k5 =
k5 = 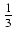 s12(2n2 + 2n - 1)
s12(2n2 + 2n - 1)
-
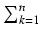 k6 =
k6 = 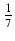 s2(3n4 +6n3 - 3n + 1)
s2(3n4 +6n3 - 3n + 1)
-
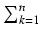 k7 =
k7 = 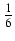 s12(3n4 +6n3 - n2 - 4n + 2)
s12(3n4 +6n3 - n2 - 4n + 2)
-
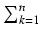 k8 =
k8 = 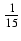 s2(5n6 +15n5 +5n4 -15n3 - n2 + 9n - 3)
s2(5n6 +15n5 +5n4 -15n3 - n2 + 9n - 3)
Sumy potęg kolejnych nieparzystych liczb naturalnych.
-
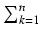 (2k - 1) = n2 =
(2k - 1) = n2 = 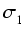
-
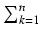 (2k - 1)2 =
(2k - 1)2 = 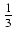 n(4n2 -1) =
n(4n2 -1) = 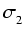
-
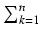 (2k - 1)3 =
(2k - 1)3 = 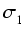 (2n2 - 1)
(2n2 - 1)
-
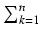 (2k - 1)4 =
(2k - 1)4 = 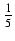
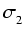 (12n2 - 7)
(12n2 - 7)
-
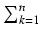 (2k - 1)5 =
(2k - 1)5 = 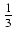
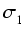 (16n4 -20n2 + 7)
(16n4 -20n2 + 7)
-
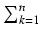 (2k - 1)6 =
(2k - 1)6 = 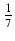
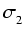 (48n4 -72n2 + 31)
(48n4 -72n2 + 31)
Podzielność.
-
2| n2 - n
-
6| n3 - n
-
30| n5 - n
-
42| n7 - n
-
546| n13 - n
-
9| 10n - 1
-
12| 10n - 4
-
11| 10n - (- 1)n
-
101| 102n - (- 1)n
-
1001| 103n - (- 1)n
-
7| 103n+1 -3(- 1)n
-
13| 103n+1 +3(- 1)n
-
14| 103n+2 -2(- 1)n
-
52| 103n+2 +4(- 1)n
-
11| 26n+1 +32n+2
-
10| 22n - 6
-
41| 5 . 72(n+1) +23n
-
25| 2n+23n + 5n - 4
-
169| 33n - 26n - 1
-
11| 55n+1 +45n+2 +35n
Nierówność Bernoulliego, jej uogólnienia i zastosowania.
-
(1 + a)n
 1 + na, a > - 1 (Bernoulli, 1689)
1 + na, a > - 1 (Bernoulli, 1689)
-
(1 + a)n
 1 + na +
1 + na + 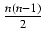 a2, a
a2, a  0
0
-
(1 + a)n
 1 + na +
1 + na + 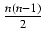 a2 +
a2 + 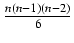 a3, a > - 1
a3, a > - 1
-
(1 + a)1/n
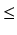 1 +
1 + 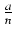 , a > - 1
, a > - 1
-
(1 + a)1+1/n
 1 +
1 + 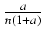 , a > - 1
, a > - 1
-
(1 + a)1+1/n
 1 + (1 +
1 + (1 + 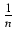 )a, a > - 1
)a, a > - 1
-
(1 + a)1+m/n
 1 + (1 +
1 + (1 + 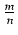 )a, a > - 1
)a, a > - 1
-
(1 + a)p/q
 1 +
1 + 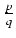 a, a > - 1,
p
a, a > - 1,
p  q
q  1
1
-
(1 + a)p/q
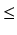 1 +
1 + 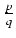 a, a > - 1,
1
a, a > - 1,
1 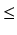 p
p 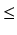 q
q
Ciąg Fibonacciego. Określamy
u0 = 0, u1 = 1,
un+2 = un + un+1
-
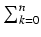 uk = un+2 - 1
uk = un+2 - 1
-
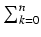 u2k+1 = u2n+2
u2k+1 = u2n+2
-
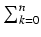 u2k = u2n+1 - 1
u2k = u2n+1 - 1
-
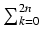 (- 1)kuk = u2n-1 - 1
(- 1)kuk = u2n-1 - 1
-
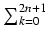 (- 1)k+1uk = u2n + 1
(- 1)k+1uk = u2n + 1
-
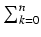 uk2 = unun+1
uk2 = unun+1
-
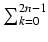 ukuk+1 = u2n2
ukuk+1 = u2n2
-
un-1un+1 - un2 = (- 1)n
-
un+1 = umun-m + um+1un-m+1,
n
 m
m  0
0
-
u2n+1 = un2 + un+12
-
u2n = un+12 - un-12
-
u3n = un3 + un+13 - un-13
-
un4 = 1 + un-2un-1un+1un+2
-
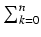
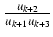 =
= 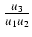 -
- 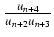
-
un =
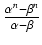 , gdzie
, gdzie 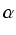 i
i 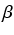 są różnymi pierwiastkami
równania
są różnymi pierwiastkami
równania
x2 = x + 1.



Next: Rachunek całkowy
Up: Ciągi liczbowe
Previous: Ciągi liczbowe
Pawel Gladki
2006-01-30
![]() . Jeśli w miejsce n
podstawimy dowolną liczbę naturalną, to T(n) stanie się zdaniem prawdziwym albo fałszywym, zależnie
od wartości n. Jeżeli, na przykład, T(n) oznacza wypowiedź "n jest podzielne przez 3", to T(6)
jest zdaniem prawdziwym, natomiast T(7) jest zdaniem fałszywym. Jeżeli T(n) oznacza nierówność n < n2,
to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej większej od 1, natomiast zdanie T(1) jest
fałszywe.
. Jeśli w miejsce n
podstawimy dowolną liczbę naturalną, to T(n) stanie się zdaniem prawdziwym albo fałszywym, zależnie
od wartości n. Jeżeli, na przykład, T(n) oznacza wypowiedź "n jest podzielne przez 3", to T(6)
jest zdaniem prawdziwym, natomiast T(7) jest zdaniem fałszywym. Jeżeli T(n) oznacza nierówność n < n2,
to T(n) jest zdaniem prawdziwym dla każdej liczby naturalnej większej od 1, natomiast zdanie T(1) jest
fałszywe.
![]() 3 spełniona jest nierówność
3 spełniona jest nierówność
![]() 3. Mnożąc tę nierówność obustronnie
przez 2 dostajemy
2 . 2n > 2 . 2n, czyli
2n+1 > 2n + 2n. Ponieważ dla każdego n
3. Mnożąc tę nierówność obustronnie
przez 2 dostajemy
2 . 2n > 2 . 2n, czyli
2n+1 > 2n + 2n. Ponieważ dla każdego n ![]() 3
mamy 2n > 2, więc
2n + 2n > 2n + 2 = 2(n + 1). Stąd ostatecznie
3
mamy 2n > 2, więc
2n + 2n > 2n + 2 = 2(n + 1). Stąd ostatecznie
![]() 3.
3.
![]() n0 jeżeli T(n) jest prawdziwe, to T(n + 1) jest prawdziwe.
n0 jeżeli T(n) jest prawdziwe, to T(n + 1) jest prawdziwe.
![]() n0
zdanie T(n) jest prawdziwe (tzw. hipoteza indukcyjna) i na tej podstawie dowodzimy prawdziwości
zdania T(n + 1).
n0
zdanie T(n) jest prawdziwe (tzw. hipoteza indukcyjna) i na tej podstawie dowodzimy prawdziwości
zdania T(n + 1).