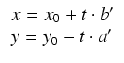Next: Jak obliczyć odwrotność liczby
Up: Liczby rzeczywiste
Previous: Jak obliczyć największy wspólny
Jak wyznaczyć liczby całkowite x i y takie, że
ax + by = c?
Rozwiązywanie równania nieoznaczonego (albo: równania diofantycznego)
ax + by = c polega
na wyznaczeniu wszystkich par (x, y) liczb całkowitych, spełniających to równanie.
Twierdzenie: Równanie diofantyczne
ax + by = c ma rozwiązanie wtedy i tylko wtedy,
gdy NWD(a, b) jest dzielnikiem liczby c.
Dowód: Oznaczmy
d = NWD(a, b) i załóżmy, że istnieje choć jedno rozwiązanie (x, y).
Skoro d jest wspólnym dzielnikiem liczb a, b, to jest również wspólnym dzielnikiem liczb ax, by,
a zatem jest też dzielnikiem ich sumy
c = ax + by.
Odwrotnie, załóżmy, że
d = NWD(a, b) jest dzielnikiem liczby c. Oznaczmy symbolem
(a, b) = {ax + by : x, y całkowite} zbiór wszystkich wartości wyrażenia
ax + by. Jest to niepusty zbiór liczb calkowitych (
a = a . 1 + b . 0 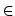 (a, b)).
Jeśli liczba ax + by jest elementem tego zbioru,
ax + by
(a, b)).
Jeśli liczba ax + by jest elementem tego zbioru,
ax + by 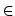 (a, b), to należy i liczba
przeciwna:
- (ax + by) = a(- x) + b(- y)
(a, b), to należy i liczba
przeciwna:
- (ax + by) = a(- x) + b(- y) 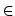 (a, b). Zatem do zbioru (a, b) należą liczby naturalne.
Inaczej: zbiór A liczb naturalnych postaci ax + by jest niepusty. Każdy niepusty zbiór liczb
naturalnych ma element najmniejszy. Niech
p = aq + bs będzie najmniejszą liczbą naturalną postaci
ax + by. Podzielmy a przez p z resztą:
(a, b). Zatem do zbioru (a, b) należą liczby naturalne.
Inaczej: zbiór A liczb naturalnych postaci ax + by jest niepusty. Każdy niepusty zbiór liczb
naturalnych ma element najmniejszy. Niech
p = aq + bs będzie najmniejszą liczbą naturalną postaci
ax + by. Podzielmy a przez p z resztą:
a =
i . p +
r i 0
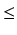 r
r <
p
skąd:
| r |
= |
a . 1 - i . p = a . 1 - a . q - b . s = |
|
| |
= |
a(1 - q) + b(- s) 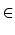 (a, b) (a, b) |
|
Ale p jest najmniejszą liczbą naturalną postaci ax + by, więc nierówność r < p oznacza, że
r nie może być liczba naturalna, musi być zerem. Czyli p jest dzielnikiem liczby a. Podobnie
sprawdzamy, że p jest dzielnikiem liczby b. W takim razie p jest dzielnikiem największego
wspólnego dzielnika d. Ale wiemy już, że d jest dzielnikiem każdej liczby postaci
ax + by, w tym liczby p. Ostatecznie p = d. To z kolei oznacza, ze
d = aq + bs 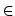 (a, b).
Zatem każda wielokrotnosc
dt = a(qt) + b(st) liczby d jest postaci ax + by - między innymi
liczba c. To kończy dowód.
(a, b).
Zatem każda wielokrotnosc
dt = a(qt) + b(st) liczby d jest postaci ax + by - między innymi
liczba c. To kończy dowód.
Twierdzenie: Jeśli para liczb całkowitych
(x0, y0) jest rozwiązaniem równania diofantycznego
ax + by = c i jeśli
d = NWD(a, b), gdzie a = a'd, b = b'd, c = c'd, to każde
rozwiązanie dane jest wzorem
dla pewnej liczby całkowitej t.
Dowód: Z jednej strony każda taka para (x, y) jest rozwiązaniem:
| ax + by |
= |
a(x0 + tb') + b(y0 - ta') = |
|
| |
= |
ax0 + by0 + (ab' - ba')t = |
|
| |
= |
c + d (a'b' - b'a')t = c. |
|
Z drugiej strony jeśli
ax + by = c i
ax0 + by0 = c, to
ax + by = ax0 + by0
a(x - x0) = b(y0 - y)
a'(x - x0) = b'(y0 - y).
Liczby a', b' są względnie pierwsze, więc jedyną możliwościa jest
x - x0 = b't, y0 - y = a' > t
dla pewnej liczby całkowitej t, co kończy dowód.
Pozostaje wskazać sposób znajdowania jednego rozwiązania
(x0, y0). W tym celu szukamy rozwiązania
równowaznego równania
a'x + b'y = c'. Najpierw rozwiązujemy pomocnicze równanie
a'u + b'v = 1.
Rozwiązaniem interesującego nas równania będzie para
(c'u, c'v).
Żeby wyznaczyć u i v stosujemy algorytm Euklidesa do liczb a' i b':
a' =
i1b' +
r1 i 0
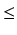 r1
r1 <
b';
b' =
i2r1 +
r2 i 0
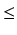 r2
r2 <
r1;
r1 =
i3r2 +
r3 i 0
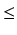 r3
r3 <
r2;
...
rm-4 =
im-2rm-3 +
rm-2 i 0
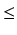 rm-2
rm-2 <
rm-3
rm-3 =
im-1rm-2 +1 i 0
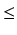
1 <
rm-2.
Teraz obliczamy kolejno od końca:
| 1 |
= |
rm-3 - im-1rm-2 = |
|
| |
= |
rm-3 - im-1(rm-4 - im-2rm-3) = |
|
| |
= |
(1 + im-1im-2)rm-3 - im-1rm-4 |
|
itd. Jeśli już udało się znaleźć przedstawienie
1 =
 rk
rk +
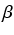 rk+1
rk+1
rk-1 = ik-3rk + rk+1
wyznaczamy resztę o największym numerze (najmniejszą z tych trzech reszt):
rk+1 = rk-1 - ik-3rk
i podstawiamy do
1 =  rk +
rk + 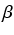 rk+1 :
rk+1 :
| 1 |
= |
 rk + rk + 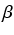 (rk-1 - ik-3rk) = (rk-1 - ik-3rk) = |
|
| |
= |
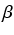 rk-1 + ( rk-1 + ( - - 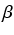 ik-3)rk. ik-3)rk. |
|
Po takim wykorzystaniu równości
a' = i1b' + r1 otrzymujemy w wyniku szukane rozwiązanie.
Przykład: wyznaczyć jedno rozwiązanie równania diofantycznego
1119x - 6778y = 1.
Najpierw algorytm Euklidesa:
-6778 = - 7 . 1119 + 1055
1119 = 1 . 1055 + 64
1055 = 16 . 64 + 31
64 = 2 . 31 + 2
31 = 15 . 2 + 1
potem podstawienia:
1 = 31 - 15 . 2
2 = 64 - 2 . 31
1 = 31 - 15 . (64 - 2 . 31) = 31 . 31 - 15 . 64
31 = 1055 - 16 . 64
1 = 31 . 31 - 15 . 64 = 31 . (1055 - 16 . 64) - 15 . 64 = 31 . 1055 - (15 + 31 . 16) . 64 = 31 . 1055 - 511 . 64
64 = 1119 - 1 . 1055
1 = 31 . 1055 - 511 . 64 = 31 . 1055 - 511 . (1119 - 1 . 1055) = (31 + 511) . 1055 - 511 . 1119 = 542 . 1055 - 511 . 1119
1055 = - 6778 + 7×1119
1 = 542 . 1055 - 511 . 1119 = 542 . (- 6778 + 7 . 1119) - 511 . 1119 = 542 . (- 6778) - (511 - 542 . 7) . 1119 = 1119 . 3283 - 6778 . 542.
Tak więc ostatecznie otrzymaliśmy:
1 = 1119 . 3283 - 6778 . 542.



Next: Jak obliczyć odwrotność liczby
Up: Liczby rzeczywiste
Previous: Jak obliczyć największy wspólny
Pawel Gladki
2006-01-30
![]() (a, b)).
Jeśli liczba ax + by jest elementem tego zbioru,
ax + by
(a, b)).
Jeśli liczba ax + by jest elementem tego zbioru,
ax + by ![]() (a, b), to należy i liczba
przeciwna:
- (ax + by) = a(- x) + b(- y)
(a, b), to należy i liczba
przeciwna:
- (ax + by) = a(- x) + b(- y) ![]() (a, b). Zatem do zbioru (a, b) należą liczby naturalne.
Inaczej: zbiór A liczb naturalnych postaci ax + by jest niepusty. Każdy niepusty zbiór liczb
naturalnych ma element najmniejszy. Niech
p = aq + bs będzie najmniejszą liczbą naturalną postaci
ax + by. Podzielmy a przez p z resztą:
(a, b). Zatem do zbioru (a, b) należą liczby naturalne.
Inaczej: zbiór A liczb naturalnych postaci ax + by jest niepusty. Każdy niepusty zbiór liczb
naturalnych ma element najmniejszy. Niech
p = aq + bs będzie najmniejszą liczbą naturalną postaci
ax + by. Podzielmy a przez p z resztą: