Czy liczb pierwszych jest nieskończenie wiele?

Tak! Pierwszy znany dowód znajduje się w Elementach Euklidesa (ok. 365 - ok. 300 pne). Przed jego przytoczeniem warto zwrócić uwagę na fakt, że u Euklidesa każde słowo jest przemyślane, i - choć dowód Euklidesa jest często przytaczany - często niedouczeni "popularyzatorzy" psują bezmyślnie to, czego nie rozumieją. Euklides nie używał zbiorów nieskończonych - pojęcie "nieskończoności aktualnej" uważano za niepewne; Euklides nie używał dowodu niewprost - taki sposób rozumowania budził (i budzi do dziś) wątpliwości natury filozoficznej. Elementy miały zawierać wiedzę absolutnie pewną. Wcześniej Euklides udowodnił, że każda liczba naturalna większa od 1 jest iloczynem liczb pierwszych. Twierdzenie Euklidesa:

O$$\iota$$  $$\pi$$$$\rho$$o$$\tau$$o$$\iota$$  $$\alpha$$$$\rho$$$$\iota$$$$\theta$$$$\mu$$o$$\iota$$  $$\pi$$$$\lambda$$$$\epsilon$$$$\iota$$o$$\nu$$$$\varsigma$$  $$\epsilon$$$$\iota$$$$\sigma$$$$\iota$$  $$\pi$$$$\alpha$$$$\nu$$$$\tau$$o$$\varsigma$$  $$\tau$$o$$\nu$$  $$\pi$$$$\rho$$o$$\tau$$$$\epsilon$$$$\theta$$$$\epsilon$$$$\nu$$$$\tau$$o$$\varsigma$$  $$\pi$$$$\lambda$$$$\eta$$$$\theta$$o$$\nu$$$$\varsigma$$  $$\pi$$$$\rho$$$$\omega$$$$\tau$$$$\omega$$$$\nu$$  $$\alpha$$$$\rho$$$$\iota$$$$\theta$$$$\mu$$o$$\nu$$

tzn. "Jest więcej liczb pierwszych, niż każda dana liczba [skończona] liczb pierwszych". I dowód:

Niech A = {p₁, p₂,..., p_n} będzie dowolnym niepustym, skończonym zbiorem liczb pierwszych. Wtedy istnieje liczba pierwsza q nie należąca do tego zbioru: niech m = p₁ ^. p2 ^. ... ^. p_n + 1. Każda z liczb p₁, p₂,..., p_n jest większa lub równa 2, wiec m > 2 - liczba m nie może być ani zerem, ani jedynką. W takim razie liczba m ma rozkład na czynniki pierwsze, w którym występuje co najmniej jedna liczba pierwsza q. Liczba q jest pierwsza i q dzieli m. W takim razie liczba q nie może być elementem zbioru A, bo dla każdego numeru i liczba m daje resztę 1 z dzielenia przez p_i.

Gdyby zbiór wszystkich liczb pierwszych był skończony, to powyższa konstrukcja pozwalałaby zbudować liczbę pierwszą, która do niego nie należy. Warto pamiętać, że sama liczba m wcale nie musi być pierwsza:

2 ^. 3 ^. 5 ^. 7 ^. 11 ^. 13 + 1 = 30031 = 59 ^. 509

Inny wariant dowodu Euklidesa:

Twierdzenie: Dla każdej liczby naturalnej n istnieje liczba pierwsza p większa od n.

Dowód: Liczba naturalna m = n! + 1 jest większa od 1, więc ma dzielnik pierwszy p. Ten dzielnik musi być większy od n, bo liczba m daje resztę 1 z dzielenia przez liczby nie przekraczające n.

Tu również sama liczba m nie musi być pierwsza: 4! + 1 = 25, 5! + 1 = 121, itd.

Jeśli znamy nieskończony ciąg liczb naturalnych parami względnie pierwszych (np. ciag n! - 1 albo 2^n!-1 - 1), to wybierając po dzielniku pierwszym każdego wyrazu tego ciągu otrzymujemy nieskończony ciąg parami różnych liczb pierwszych.

Później (od XVII w.) podano inne dowody faktu, że liczb pierwszych jest nieskończenie wiele. Jednym z nich jest dowód Eulera - oznaczmy mianowicie przez p_n n -tą liczbę pierwszą. Euler udowodnił, że szereg odwrotności liczb pierwszych:

$$\sum_{{n=1}}^{{\infty}}$$$${\frac{{1}}{{p_n}}}$$

jest rozbieżny; to automatycznie pociąga fakt, że liczb pierwszych jest nieskończenie wiele - w przeciwnym razie powyższa suma byłaby skończoną sumą ułamków, a więc liczbą skończoną. Oryginalny dowód Eulera wykorzystywał rozwinięcie $\zeta$-funkcji Riemanna na iloczyn Eulera. My podamy trochę inny dowód tego faktu.

Niech $\pi$(n) oznacza liczbę liczb pierwszych mniejszych lub równych od n. W takim razie p₁, p₂,..., p_$\pi$(n) są wszystkimi liczbami pierwszymi mniejszymi lub równymi n. Oznaczmy ponadto:

$$\lambda$$(n) = $$\prod_{{i=1}}^{{\pi(n)}}$$(1 - $${\frac{{1}}{{p_i}}}$$)^-1.

Korzystając ze wzoru na sumę szeregu geometrycznego o ilorazie ${\frac{{1}}{{p_i}}}$:

$$\sum_{{a_i = 0}}^{{\infty}}$$$${\frac{{1}}{{p_i^{a_i}}}}$$ = (1 - $${\frac{{1}}{{p_i}}}$$)^-1

możemy przekształcić wzór na $\lambda$(n) w następujący sposób: niech A oznacza zbiór wszystkich ciągów (a₁, a₂,..., a_l(n)) liczb całkowitych nieujemnych. Wówczas:

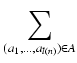$$\lambda$$(n) = $$\prod_{{i=1}}^{{\pi(n)}}$$$$\sum_{{a_i = 0}}^{{\infty}}$$$${\frac{{1}}{{p_i^{a_i}}}}$$ = $$\sum_{{(a_1, \ldots, a_{l(n)}) \in A}}^{}$$(p₁^a₁p₂^a₂...p_$\pi$(n)^a_l(n))^-1.

Zatem każda liczba całkowita k $\leq$ n ma wszystkie czynniki pierwsze nie przekraczające n, więc ${\frac{{1}}{{k}}}$ jest jednym ze składników sumy po prawej stronie. Pozostałe składniki są dodatnie, skąd:

$${\frac{{1}}{{1}}}$$ + $${\frac{{1}}{{2}}}$$ +...+ $${\frac{{1}}{{n}}}$$ < $$\lambda$$(n),

a stąd wynika, że $\lim_{{n \rightarrow \infty}}^{}$$\lambda$(n) = $\infty$.

Zajmijmy się teraz oszacowaniem ln$\lambda$(n) od góry. Rozwijając w szereg Tayloga funkcję ln(1 - x) dla -1 $\leq$ x < 1 dostajemy:

ln(1 - x) = - $$\sum_{{m=1}}^{{\infty}}$$$${\frac{{x^m}}{{m}}}$$.

Stąd:

$$\lambda \sum_{{i=1}}^{{\pi(n)}} {\frac{{1}}{{p_i}}} \sum_{{i=1}}^{{\pi(n)}} \sum_{{m=1}}^{{\infty}}$$ =

$${\frac{{1}}{{p_1}}} {\frac{{1}}{{p_2}}} {\frac{{1}}{{p_{\pi(n)}}}} \sum_{{i=1}}^{{\pi(n)}} \sum_{{m=2}}^{{\infty}}$$ =

Ponieważ:

$$\sum_{{m=2}}^{{\infty}}$$(mp_i^m)^-1 < $$\sum_{{m=2}}^{{\infty}}$$(p_i^m)^-1 = p_i^-2(1 - $${\frac{{1}}{{p_i}}}$$)^-1 $$\leq$$ 2p_i^-2,

więc drugi składnik w poprzednim wzorze spełnia nierówności:

$$\sum_{{i=1}}^{{\pi(n)}}$$$$\sum_{{m=2}}^{{\infty}}$$(mp_i^m)^-1 < 2$$\sum_{{i=1}}^{{\pi(n)}}$$p_i^-2 < 2$$\sum_{{m=1}}^{n}$$m^-2.

Wobec tego:

ln$$\lambda$$(n) < ($${\frac{{1}}{{p_1}}}$$ + $${\frac{{1}}{{p_2}}}$$ +...+ $${\frac{{1}}{{p_{\pi(n)}}}}$$) + 2($${\frac{{1}}{{p_1^2}}}$$ + $${\frac{{1}}{{p_2^2}}}$$ +...+ $${\frac{{1}}{{p_{\pi(n)}^2}}}$$).

Jak wiadomo szereg $\sum_{{m=1}}^{{\infty}}$${\frac{{1}}{{m^2}}}$ jest zbieżny (do liczby ${\frac{{\pi^2}}{{6}}}$), a więc drugi składnik w powyższej sumie nie może przekroczyć liczby ${\frac{{\pi^2}}{{3}}}$ niezależnie od wartości liczby n. Tak więc gdyby szereg odwrotności liczb pierwszych był zbieżny, to również funkcja n $\mapsto$ ln$\lambda$(n) byłaby ograniczona, co stoi w sprzeczności z wcześniej stwierdzoną równością $\lim_{{n \rightarrow \infty}}^{}$$\lambda$(n) = $\infty$.

To, że jest nieskończenie wiele liczb pierwszych wynika też wprost z twierdzenia Czebyszewa o liczbach pierwszych z 1850 roku. Warto również wspomnieć, iż Dirichlet udowodnił, że w każdym ciągu arytmetycznym:

a_n = a₁ + (n - 1)r

w którym NWD(a₁, r) = 1, nieskończenie wiele wyrazów to liczby pierwsze.