Spójnik logiczny k-argumentowy to dowolna funkcja
0, 1k ![]() 0, 1. Spójnik
nazwiemy uniwersalnym, jeśli przez składanie go ze sobą i ewentualnie wielokrotne
podstawianie argumentów da się otrzymać wszystkie spójniki logiczne o dowolnej liczbie
argumentów.
0, 1. Spójnik
nazwiemy uniwersalnym, jeśli przez składanie go ze sobą i ewentualnie wielokrotne
podstawianie argumentów da się otrzymać wszystkie spójniki logiczne o dowolnej liczbie
argumentów.
Scharakteryzować wszystkie spójniki uniwersalne i obliczyć granicę
![]()
![]() , gdzie Uk to liczba spójników uniwersalnych
k -argumentowych, Sk - liczba wszystkich spójników k -argumentowych.
, gdzie Uk to liczba spójników uniwersalnych
k -argumentowych, Sk - liczba wszystkich spójników k -argumentowych.
Spróbujemy oszacować granicę od dołu.
Wiadomo, że z dwuargumentowych NAND lub NOR można zrobić wszystko. Trzeba by więc zastanowić się, z ilu k -spójników można zrobić dwuargumentowe NAND lub NOR, czyli ile co najmniej jest uniwersalnych.
Polega to na podzieleniu k argumentów na dwie niepuste grupy x i y oraz za argumenty w jednej grupie podstawiać pierwszy parametr, a za argumenty w drugiej grupie - drugi parametr dwuargumentowego NAND-a lub NOR-a, którym będzie nasz spójnik k-argumentowy.
Takich podziałów jest
![]() (mają być niepuste i nie jest ważna
kolejność).
(mają być niepuste i nie jest ważna
kolejność).
Wystarczy, że dla jednego z nich spójnik zachowuje się jak NAND albo NOR.
Rozważmy wszystkie spójniki dające 1 dla samych zer (zera w całej grupie x i y) i 0 dla samych jedynek (jedynki w całej grupie x i y), czyli tak jak NAND i NOR dla takich argumentów, dla pozosta?ych 2k - 2 kombinacji, 0 lub 1. Jest ich:
dzielą się one na takie, które dla żadnego podziału na grupy nie zachowują się ani jak NAND ani jak NOR (pozostają tylko dwie możliwości, z założenia w poprzednim akapicie, stąd 2 w podstawie potęgi)
oraz takie, które dla przynajmniej jednego podziału zachowują się jak dwuargumentowe NAND i NOR, z których można zrobić każdą funkcję logiczną. Tych właśnie szukamy, jest ich oczywiście
Iloraz
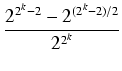
dąży od dołu do 1/4.
Charakteryzacja spójników uniwersalnych wygląda natomiast tak: (niech ![]() 0 = 1,
0 = 1, ![]() 1 = 0,
1 = 0,
![]() (a1, a2,..., ak) = (
(a1, a2,..., ak) = (![]() a1,
a1,![]() a2,...,
a2,...,![]() ak) dla
a1, a2,..., ak
ak) dla
a1, a2,..., ak ![]() 0, 1).
0, 1).
N-argumentowy spójnik A jest uniwersalny, gdy:
Uzasadnienie:
Jeśli byłoby A(0, 0,..., 0) = 0, to każde wyrażenie zbudowane tylko z użyciem spójnika A miałoby wartość 0, gdyby wszystkie zmienne miały wartość 0 (formalny dowód - indukcja ze względu na budowę wyrażenia). Nie udałoby nam się więc zrobić jednoargumentowego NOTa.
Jeśli byłoby A(1, 1,..., 1) = 1, to każde wyrażenie zbudowane tylko z użyciem spójnika A miałoby wartość 1, gdyby wszystkie zmienne miały wartość 1 (formalny dowód - indukcja ze względu na budowę wyrażenia). Nie udałoby nam się więc zrobić jednoargumentowego NOTa.
Jeśli dla wszystkich
(a1, a2,..., aN), gdzie ai równa się 0 lub 1 byłoby
A(a1, a2,..., aN) = ![]() A(
A(![]() (a1, a2,..., aN)), to dla każdego wyrażenia
zbudowanego tylko z użyciem spójnika A zamiana wartości wszystkich zmiennych na
przeciwne (0 na 1, 1 na 0) powodowałaby również zmianę wyniku na przeciwny (formalny
dowód - indukcja ze względu na budowę wyrażenia). Nie udałoby nam się więc zrobić na
przykład dwuargumentowego ANDa.
(a1, a2,..., aN)), to dla każdego wyrażenia
zbudowanego tylko z użyciem spójnika A zamiana wartości wszystkich zmiennych na
przeciwne (0 na 1, 1 na 0) powodowałaby również zmianę wyniku na przeciwny (formalny
dowód - indukcja ze względu na budowę wyrażenia). Nie udałoby nam się więc zrobić na
przykład dwuargumentowego ANDa.
Niech teraz A spełnia warunki
Ustalmy jedną N-ke (a1, a2,..., aN) jak wyżej. Niech W(x, y) = A(z1, z2,..., zN), gdzie zi = x, gdy ai = 0 oraz zi = y, gdy ai = 1. W(x, y) jest dwuargumentowym NORem, jeśli
Scharakteryzowaliśmy więc wszystkie spójniki uniwersalne i są to dokładnie te, które już zostały policzone w notce. Ich liczba to UN = 22N-2 -2(2N-2)/2 .
Lech Duraj, Andrzej Komisarski, Michał Śliwka, styczeń, październik, listopad 2004
Linki do oryginalnych dyskusji: [1], [2]