
Link do powyższego złudzenia optycznego pojawia się dość często na łamach pl.sci.matematyki... Normalny
człowiek widzi coś, co wydaje mu się trójkątem i krzyczy "trójkąt!" - matematyk, przed wydaniem takiego
radosnego okrzyku upewnia się, że to co widzi, faktycznie jest trójkątem. W tym przypadku - oczywiście tak
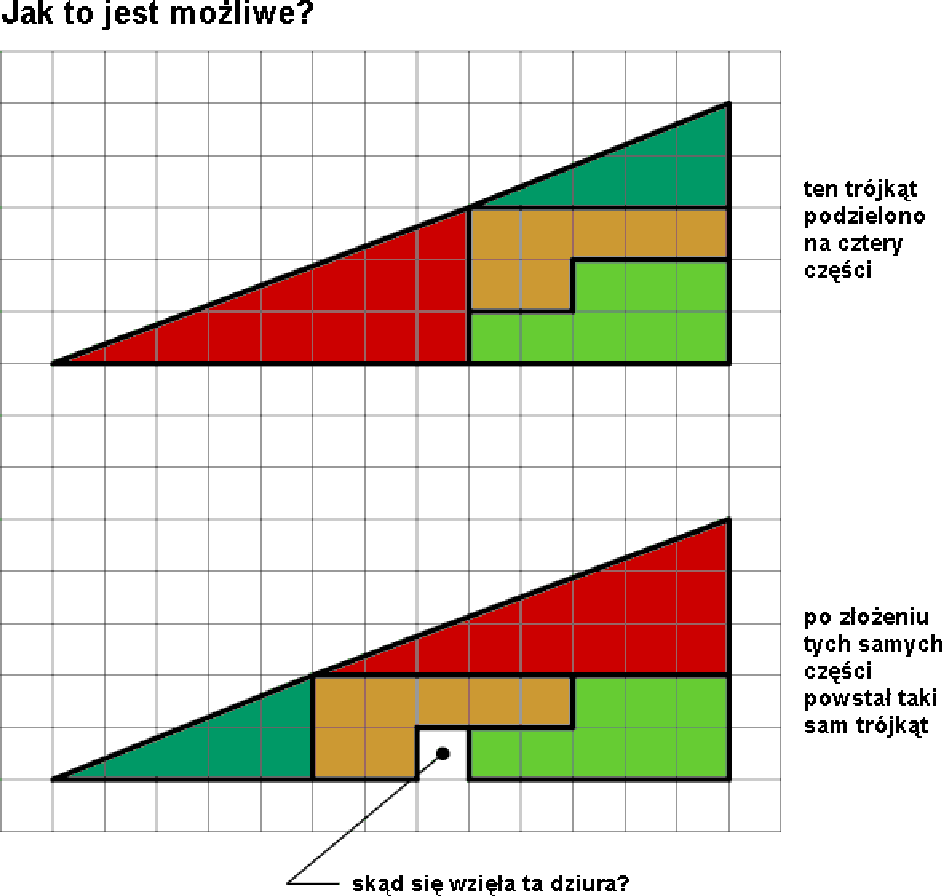
nie jest. Przyjrzyjmy się dwóm figurom występującym na obrazku - czerwonej i zielonej. Nie ulega wątpliwości,
że obydwie są trójkątami (jako obszary ograniczone trzema odcinkami). Obliczmy zatem tangensy ich kątów
ostrych po lewej stronie - dla trójkąta zielonego jest to
![]() , a dla czerwonego
, a dla czerwonego
![]() .
Oczywiście
.
Oczywiście
![]()
![]()
![]() - a więc zarówno figura u góry obrazka jak i figura u dołu obrazka
nie może być trójkątem (gdyby była, kąty ostre trójkątów zielonego i czerwonego, a więc i ich tangensy,
musiałyby być takie same). W szczególności nie możemy liczyć pola górnego "trójkąta" dzieląc na połowę
iloczyn podstawy i wysokości - trzeba zamiast tego dodać do siebie pola składowych figur; wówczas
przekonamy się, że pola "trójkątów" górnego i dolnego są takie same i że niczego na rysunku nie brakuje.
- a więc zarówno figura u góry obrazka jak i figura u dołu obrazka
nie może być trójkątem (gdyby była, kąty ostre trójkątów zielonego i czerwonego, a więc i ich tangensy,
musiałyby być takie same). W szczególności nie możemy liczyć pola górnego "trójkąta" dzieląc na połowę
iloczyn podstawy i wysokości - trzeba zamiast tego dodać do siebie pola składowych figur; wówczas
przekonamy się, że pola "trójkątów" górnego i dolnego są takie same i że niczego na rysunku nie brakuje.
Faktycznie, po dokładniejszym się przyjrzeniu wprawne oko może zauważyć, że przy przy połączeniu trójkąta zielonego i czerwonego "przeciwprostokątna" naszego "trójkąta" nieznacznie się załamuje...