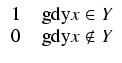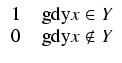Next: Inne często spotykane schematy
Up: Elementy kombinatoryki
Previous: Wariacje z powtórzeniami
Ograniczymy się do kilku popularnych przykładów:
- Pemutacja zbioru
{1, 2,..., n} jest n-wyrazową wariacją bez powtórzeń n elementów i
|
Sn| =
n! =
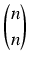 n
n! =
Vnn
- k-wyrazowa wariacja n-elementów wyznacza kombinację n elementów po k - wystarczy
zapomnieć o kolejności elementów, czyli przyporządkować funkcji różnowartościowej
f : 1, 2,..., k
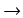 {1, 2,..., n} jej obraz (zbiór wartości). Wariacje bez powtórzeń
wyznaczające tę samą kombinację różnią się kolejnością wyrazów, więc jedna kombinacja daje k!
wariacji. Zatem
{1, 2,..., n} jej obraz (zbiór wartości). Wariacje bez powtórzeń
wyznaczające tę samą kombinację różnią się kolejnością wyrazów, więc jedna kombinacja daje k!
wariacji. Zatem
Vnk =
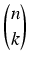 k
k! =
Cnkk!
- Zbiór wszystkich podzbiorów zbioru X oznaczamy 2X i nazywamy zbiorem potęgowym zbioru X.
Jeśli zbiór X ma n elementów, | X| = n, to liczbę jego podzbiorów | 2X| można obliczyć tak:
| 2
X| =
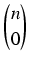
+
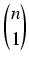
+...+
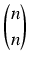
= (1 + 1)
n = 2
n = 2
| X|
fY(
x) =
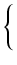
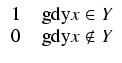
Zatem
| 2X| = Wn2 = 2n = 2| X|.
Wzór
| 2X| = 2| X|
jest (z definicji) prawdziwy dla dowolnego zbioru X.



Next: Inne często spotykane schematy
Up: Elementy kombinatoryki
Previous: Wariacje z powtórzeniami
Pawel Gladki
2006-01-30
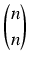 n! = Vnn
n! = Vnn
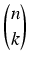 k! = Cnkk!
k! = Cnkk!
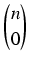 +
+ 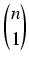 +...+
+...+ 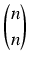 = (1 + 1)n = 2n = 2| X|
= (1 + 1)n = 2n = 2| X|