


Next: Wariacje z powtórzeniami
Up: Elementy kombinatoryki
Previous: Permutacje
Zbiór wszystkich funkcji różnowartościowych zbioru k-elementowego w zbiór n-elementowy.
Funkcje różnowartościowe określone w zbiorze k-elementowym o wartościach w zbiorze n-elementowym
nazywamy k-wyrazowymi wariacjami bez powtórzen n elementów. Dla pary liczb naturalnych n, k
liczbę elementów zbioru k-wyrazowych wariacji bez powtórzeń n elementów oznaczamy Vnk.
Jeśli zbiorem k-elementowym jest zbiór
{1, 2,..., k}, to wariacja bez powtórzeń f jest
ciągiem k-wyrazowym
(f (1), f (2),..., f (k)) elementów zbioru n-elementowego.
Liczba Vnk k-wyrazowych wariacji bez powtórzeń n elementów wyraża się wzorem
Vnk =
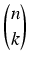 k
k! =
n(
n - 1)...(
n -
k + 1).
W szczególności jeśli k > n, to Vnk = 0. Rzeczywiście, jeśli k = 0 lub k = 1 to łatwo
sprawdzić, że liczba
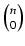 0! = 1 jest liczbą Vn0 pustych ciagów elementów zbioru
n-elementowego,
0! = 1 jest liczbą Vn0 pustych ciagów elementów zbioru
n-elementowego,
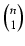 1! = n jest liczbą Vn1 jednowyrazowych ciagów elementów
zbioru n-elementowego. Jeśli dla pewnej liczby k zachodzi równość
1! = n jest liczbą Vn1 jednowyrazowych ciagów elementów
zbioru n-elementowego. Jeśli dla pewnej liczby k zachodzi równość
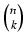 k! = n, to każdy
ciąg k-wyrazowy można przedłużyć do ciągu (k + 1)-wyrazowego na tyle sposobów, ile elementów
zbioru n-elementowego nie występuje w tym ciągu, czyli na n - k sposobów. Łącznie jest więc
k! = n, to każdy
ciąg k-wyrazowy można przedłużyć do ciągu (k + 1)-wyrazowego na tyle sposobów, ile elementów
zbioru n-elementowego nie występuje w tym ciągu, czyli na n - k sposobów. Łącznie jest więc
Vnk+1 = (
n -
k)
Vnk = (
n -
k)
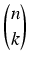 k
k! =
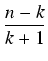
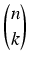
(
k + 1)! =
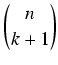
(
k + 1)!
ciągów (k + 1)-wyrazowych i wzór na liczbę wariacji bez powtórzeń jest słuszny dla wszystkich
liczb naturalnych k.



Next: Wariacje z powtórzeniami
Up: Elementy kombinatoryki
Previous: Permutacje
Pawel Gladki
2006-01-30
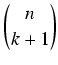 (k + 1)!
(k + 1)!